Image Source:
(2024). Britannica.com. https://cdn.britannica.com/28/252328-050-C65E7F72/capital-asset-pricing-model.jpg
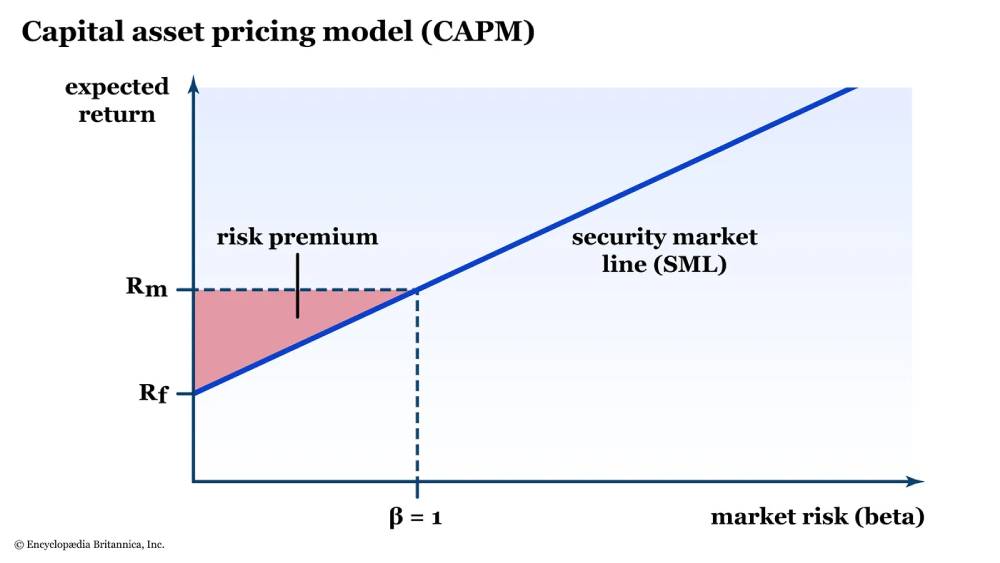
The Capital Asset Pricing Model (CAPM) is a widely used financial model that helps investors and analysts understand the relationship between risk and expected return for individual securities or portfolios. It provides a framework for calculating the expected return on an investment based on its risk relative to the overall market.
Here’s how the CAPM works:
1. **Expected Return**: The CAPM calculates the expected return of an investment as the sum of the risk-free rate (typically the yield on government bonds) and a risk premium.
2. **Risk Premium**: The risk premium is the product of the asset’s beta (β) and the market risk premium. Beta measures the volatility of an asset relative to the market. If an asset has a beta of 1, it moves in tandem with the market. If it’s less than 1, it’s less volatile than the market, and if it’s greater than 1, it’s more volatile.
3. **Formula**: The CAPM formula is:
\[ E(R_i) = R_f + \beta_i \times (E(R_m) – R_f) \]
Where:
– \(E(R_i)\) is the expected return on the investment.
– \(R_f\) is the risk-free rate.
– \(\beta_i\) is the beta of the investment.
– \(E(R_m)\) is the expected return on the market.
– \(E(R_m) – R_f\) is the market risk premium.
4. **Interpretation**: The CAPM helps investors assess whether an investment offers a fair return given its risk level. If the expected return calculated using CAPM is higher than the required return, the investment may be considered attractive. Conversely, if it’s lower, the investment may be deemed too risky for the potential return.
5. **Applications**: The CAPM is widely used in portfolio management, asset pricing, and investment decision-making. It provides a standardized method for estimating the expected returns of various investments, enabling investors to make informed decisions based on risk-return trade-offs.
Let’s work through a numeric example to illustrate how the Capital Asset Pricing Model (CAPM) is used to calculate the expected return on an investment.
### Example:
Suppose we have the following information:
– Risk-free rate (\( R_f \)): 3%
– Expected return on the market (\( E(R_m) \)): 10%
– Beta (\( \beta_i \)) of the investment: 1.5
### Calculation:
Using the CAPM formula:
\[ E(R_i) = R_f + \beta_i \times (E(R_m) – R_f) \]
We can plug in the values:
\[ E(R_i) = 0.03 + 1.5 \times (0.10 – 0.03) \]
\[ E(R_i) = 0.03 + 1.5 \times 0.07 \]
\[ E(R_i) = 0.03 + 0.105 \]
\[ E(R_i) = 0.135 \]
### Interpretation:
So, the expected return (\( E(R_i) \)) on the investment, calculated using the CAPM, is 13.5%.
This means that, according to the CAPM, investors would expect to earn a return of 13.5% on this investment given its risk level (as measured by its beta) relative to the market and the prevailing risk-free rate. If the investment were to offer a return higher than 13.5%, it might be considered attractive, whereas if it were to offer a lower return, it might be deemed less attractive relative to its risk.
While the CAPM has its critics and limitations, it remains a valuable tool for financial analysts and investors in understanding and assessing investment opportunities.