Understanding Indefinite and Definite Integrals in Economics and Beyond

Introduction
Integral calculus is a cornerstone of mathematical analysis with profound applications in economics, physics, and engineering. While differentiation is about rates of change, integration is about accumulation: summing infinitesimal changes to understand totals. This blog post provides a clear yet academically grounded introduction to indefinite and definite integrals, with a focus on intuitive understanding and economic relevance.

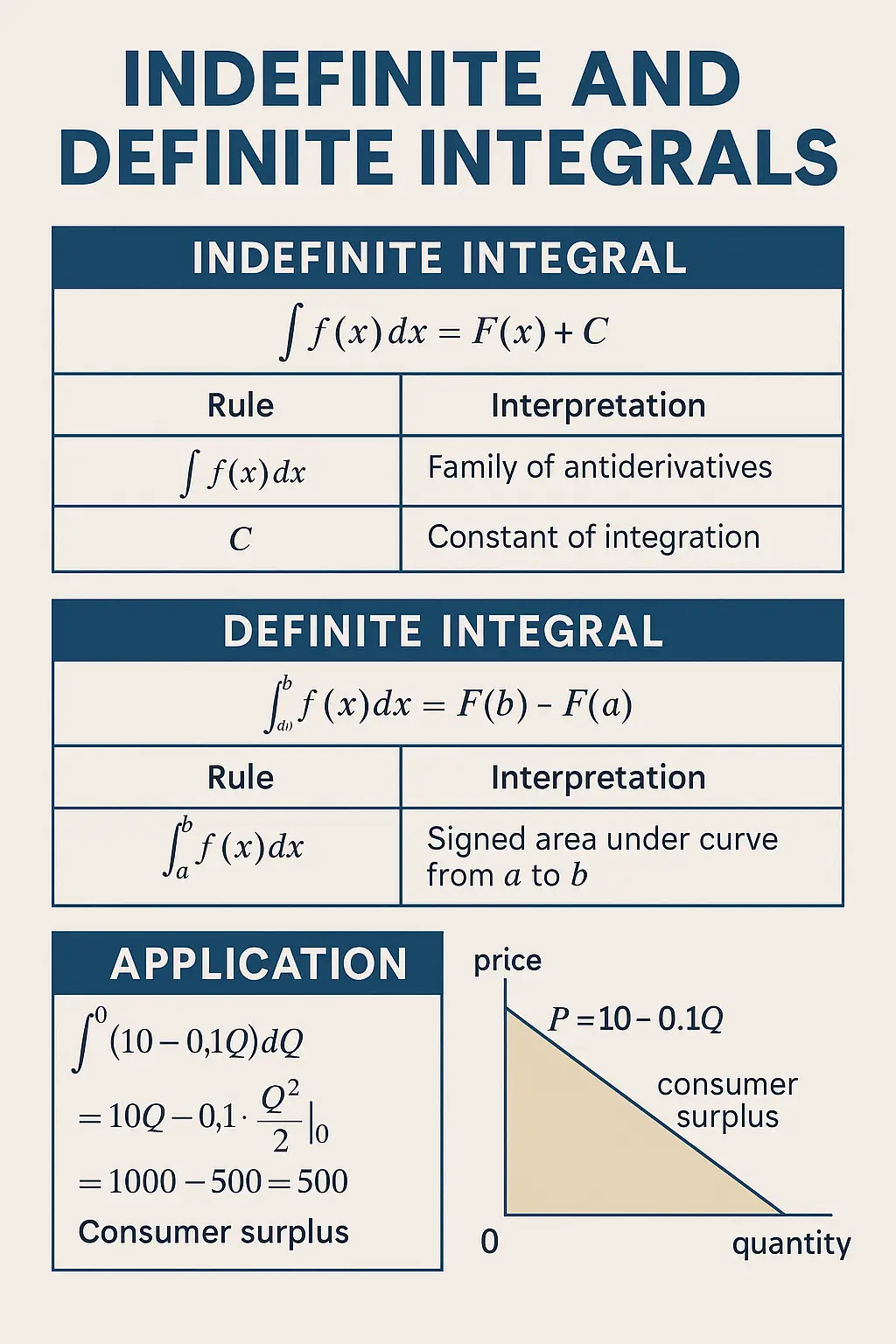
1. What Is an Indefinite Integral?
An indefinite integral represents a family of functions whose derivatives equal the given function. In other words, it reverses differentiation.

Definition:

Given a function $f(x)$, its indefinite integral is:
$\int f(x)\,dx = F(x) + C$
where:

• $F(x)$ is any antiderivative of $f(x)$
• $C$ is the constant of integration

Example:

$\int 3x^2 dx = x^3 + C$

This means that any function of the form $x^3 + C$ has a derivative of $3x^2$.

2. Common Rules and Techniques

• $\int x^n dx = \frac{x^{n+1}}{n+1} + C$ (for $n \neq -1$)
• $\int e^x dx = e^x + C$
• $\int \frac{1}{x} dx = \ln|x| + C$

Techniques include:

• Substitution (change of variables)
• Integration by parts
• Partial fractions (for rational functions)

These help solve more complex expressions and are particularly useful in economic models with composite cost or utility functions.

3. What Is a Definite Integral?
A definite integral computes the net area under a curve over an interval $[a, b]$. It gives a numerical value representing total accumulation.

Definition:

$\int_a^b f(x) dx = F(b) – F(a)$
where $F$ is any antiderivative of $f$.

Interpretation:

• Area under the curve when $f(x) \geq 0$
• Net accumulation when $f(x)$ may cross the x-axis

4. Applications in Economics
Integration helps us move from marginal to total concepts:

• Total cost from marginal cost: $C(q) = \int MC(q)\,dq$
• Total revenue from marginal revenue: $R(q) = \int MR(q)\,dq$
• Consumer surplus:
  $CS = \int_0^Q D(q) dq – P \cdot Q$

These integrals measure accumulated benefit or cost, vital in evaluating policies, pricing strategies, and welfare.

5. Indefinite vs. Definite Integrals: Key Differences

6. The Fundamental Theorem of Calculus
This links the two types of integrals:

• Part 1: If $F(x) = \int_a^x f(t) dt$, then $F'(x) = f(x)$
• Part 2: $\int_a^b f(x) dx = F(b) – F(a)$

This theorem ensures that differentiation and integration are inverse processes — a core concept in mathematical economics and optimization.

7. Example in Practice
Let $MC(q) = 2q + 5$. Then:
$TC(q) = \int (2q + 5) dq = q^2 + 5q + C$

If $TC(0) = 0$, then $C = 0$, so:
$TC(q) = q^2 + 5q$

This gives us the total cost of producing $q$ units based on marginal cost.

Conclusion
Integrals allow economists, scientists, and engineers to model accumulated effects, from profit and cost to pollution and population. By understanding the distinction between indefinite and definite integrals — and mastering the tools to compute them — students can unlock powerful insights across disciplines.

Whether you’re evaluating total revenue, calculating consumer surplus, or tracing cumulative trends, integration is the bridge between marginal decisions and total impact.

Further Reading

• Stewart, J. (2015). Calculus: Early Transcendentals
• Chiang & Wainwright. Fundamental Methods of Mathematical Economics