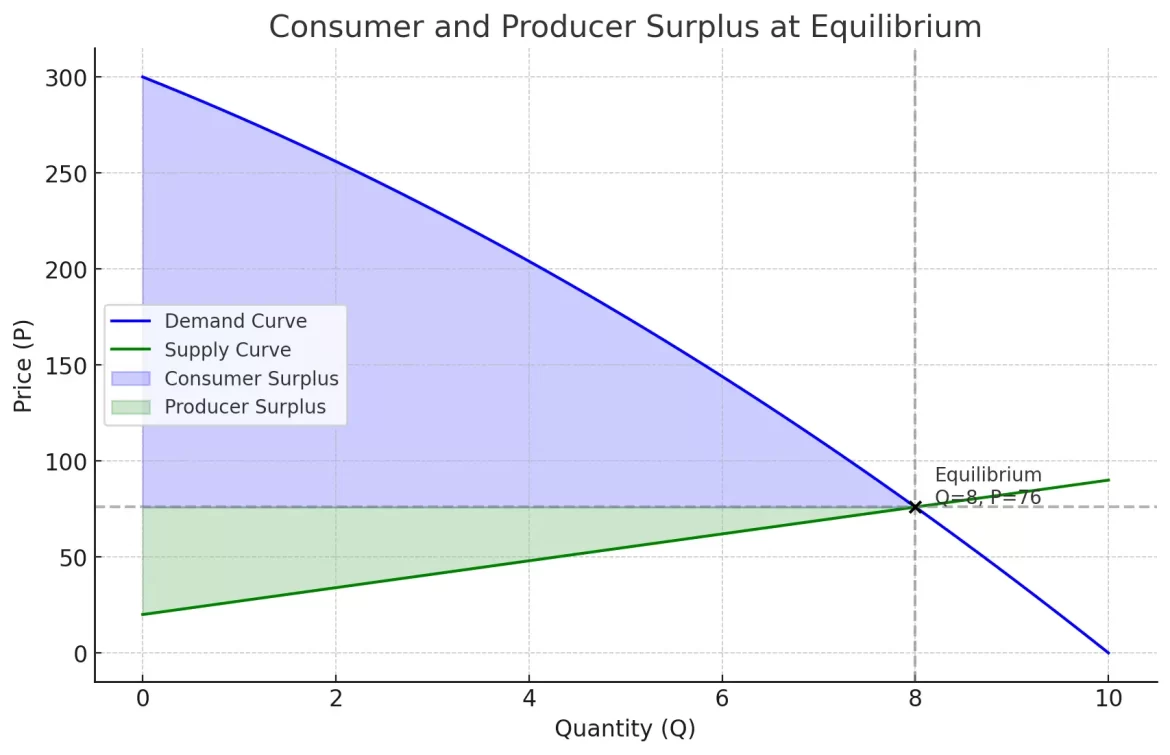
Consumer and Producer Surplus at Equilibrium

Consumer and Producer Surplus at Equilibrium

The following demand and supply functions are given:

• Demand function (price as a function of quantity):

  $$P_d = 300 – 20Q – Q^2$$

• Supply function:

  $$P_s = 20 + 7Q$$

Questions

(a) Determine the domain of the demand function given that it is decreasing. Then find the equilibrium price and quantity.
(b) Calculate the consumer surplus at equilibrium.
(c) Calculate the producer surplus at equilibrium.

Solutions

(a) Domain and Equilibrium

Step 1: Domain of the Demand Function

Given:

$$P_d = 300 – 20Q – Q^2$$

This is a quadratic function opening downward (because the coefficient of $Q^2$ is negative). The function is decreasing as long as we stay to the left of the vertex.

The vertex of a quadratic $ax^2 + bx + c$ occurs at:

$$Q = -\frac{b}{2a} = -\frac{-20}{2(-1)} = \frac{20}{-2} = -10$$

But this is not valid, because negative quantities make no economic sense here. Since we want the decreasing part, we only consider values before the vertex, so for:

$$Q \in [0, 10]$$

Step 2: Find Equilibrium

Set $P_d = P_s$:

$$300 – 20Q – Q^2 = 20 + 7Q$$

Move all terms to one side:

$$300 – 20Q – Q^2 – 20 – 7Q = 0 \Rightarrow -Q^2 – 27Q + 280 = 0$$

Multiply through by -1:

$$Q^2 + 27Q – 280 = 0$$

Solve using the quadratic formula:

$$Q = \frac{-27 \pm \sqrt{27^2 + 4 \cdot 280}}{2} = \frac{-27 \pm \sqrt{729 + 1120}}{2} = \frac{-27 \pm \sqrt{1849}}{2} = \frac{-27 \pm 43}{2}$$ $$Q_1 = \frac{-27 + 43}{2} = 8 \quad \text{(valid)} \quad Q_2 = \frac{-27 – 43}{2} = -35 \quad \text{(not valid)}$$

So, equilibrium quantity is $Q = 8$

Substitute into either function to find price:

$$P = 20 + 7(8) = 20 + 56 = 76$$

Or:

$$P = 300 – 20(8) – 8^2 = 300 – 160 – 64 = 76$$

✅ Equilibrium is at $Q = 8$, $P = 76$

(b) Consumer Surplus

Consumer surplus is the area between the demand curve and the price, up to the equilibrium quantity.

Use the integral of the demand function from $0$ to $Q^* = 8$, minus the rectangle $P \cdot Q$:

$$CS = \int_0^8 (300 – 20Q – Q^2) \, dQ – 76 \cdot 8$$

Integrate:

$$\int_0^8 (300 – 20Q – Q^2) \, dQ = \left[300Q – 10Q^2 – \frac{1}{3}Q^3\right]_0^8$$

Substitute $Q = 8$:

$$= 300(8) – 10(64) – \frac{1}{3}(512) = 2400 – 640 – \frac{512}{3} = 1760 – \frac{512}{3} = \frac{5280 – 512}{3} = \frac{4768}{3} \approx 1589.33$$

Rectangle area (expenditure):

$$76 \cdot 8 = 608$$

So:

$$CS = 1589.33 – 608 = 981.33$$

✅ Consumer Surplus ≈ 981.33

(c) Producer Surplus

Producer surplus is the area between the price and the supply curve, up to the equilibrium quantity:

$$PS = 76 \cdot 8 – \int_0^8 (20 + 7Q) \, dQ$$

Calculate the integral:

$$\int_0^8 (20 + 7Q) \, dQ = \left[20Q + \frac{7}{2}Q^2\right]_0^8 = 20(8) + \frac{7}{2}(64) = 160 + 224 = 384$$

Rectangle area:

$$76 \cdot 8 = 608$$

So:

$$PS = 608 – 384 = 224$$

✅ Producer Surplus = 224

Final Answers

• Equilibrium: $Q = 8$, $P = 76$
• Consumer Surplus: ≈ 981.33
• Producer Surplus: 224