97
Linear Systems Exercise
(a) Solve the following system of equations:
(b) Consider the following system of equations:
Use the Gaussian elimination method to determine its solutions, if they exist.
Solutions
(a) Solve the 2×2 system
We have:
Step 1: Express in terms of from equation (1):
Step 2: Substitute into equation (2):
Step 3: Substitute back to find :
✅ Solution:
(b) Gaussian elimination
The system:
Write the augmented matrix:
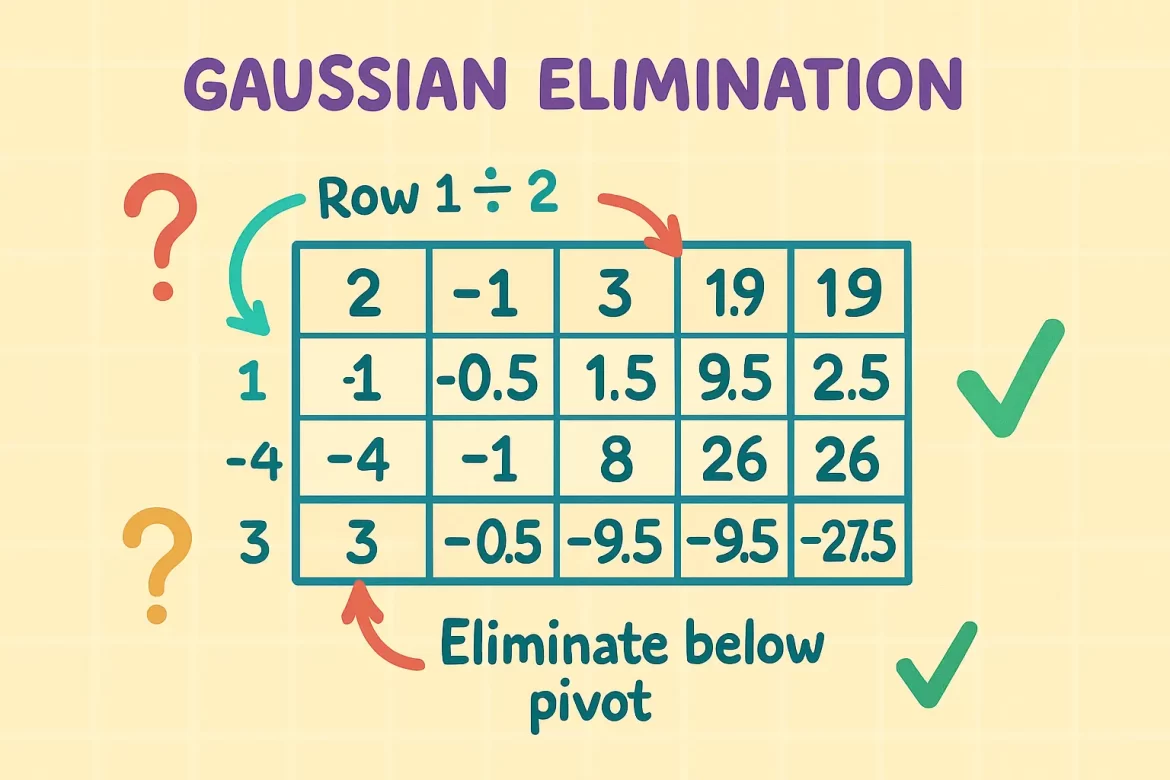
Step 1: Make first pivot = 1 (Row 1 ÷ 2):
Step 2: Eliminate below pivot
- Row 2:
- Row 3:
Result:
Step 3: Make second pivot = 1 (Row 2 ÷ -1):
Step 4: Eliminate below pivot
- Row 3:
Result:
Step 5: Back substitution
From Row 3:
From Row 2:
From Row 1:
✅ Solution:
Final Answers
- (a) Solution: ,
- (b) Solution: , ,